Kaffe och kluring: Ett noll-trick del två

Spoiler alert! Nedan kommer vi att lösa kluringen från förra inlägget.

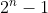
I förra inlägget visade vi på en faktor $2^m-1$ i uttrycket $2^n-1$ . Vi skall nu hitta en faktor till och på så vis vara klara med beviset i ena riktningen. Vi hade speciellt att

$2^n -1 = (2^m-1) \times (1+2^m+ 2^{2m} \cdots + 2^{(n/m-1)m}) =\\ (2^m-1) \times (1+2^m+ (2^m)^2 \cdots + (2^m)^{(n/m-1)}).$

Låt oss till varje term $(2^m)^j$ addera 0 = 1 - 1:

$(2^m)^j - 1 + 1 = (2^m - 1)\times (1+2^m + (2^m)^2+(2^m)^{j-1}) + 1$ .

Eftersom vi har n/m -1 +1 termer har vi adderat 0 n/m gånger vilket enligt antagandet är en multipel av $2^m-1$ . Varje term ger med "noll-tricket" en multipel av $2^m-1$ och en term 1. Vi har nu hittat ytterligare en term $2^m-1$ och är klara med ena riktningen. Efter en stunds tänkande kommer vi fram till att varje steg är ekvivalent med det föregående och har således även andra riktningen av beviset. Puh!

Kaffe och kluring

lördag 23 november 2019

Ett noll-trick del två

Inga kommentarer:

Skicka en kommentar